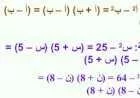طريقة حساب محيط المثلث
يمكن حساب محيط المثلث عن طريق جمع جميع أطوال أضلاعه المكوّنة له؛ فإذا كانت أطوال أضلاع المثلث هي: أ، ب، ج، فإن محيط المثلث= أ+ب+ج، وهو مساوٍ لمجموع أطوال جميع أضلاعه، وفي حالة المثلث متساوي الأضلاع فإن محيطه= 3 * قياس أحد الأضلاع، والمحيط هو في حد ذاته طول، وبالتالي فإنّ وحدة قياسه هي وحدة قياس الطول؛ أي متر، أو سنتيمتر، أو ملليمتر، أو غيرها.[١] ويمتلك المثلث ثلاثة أضلاع وثلاث زوايا، ويساوي مجموع زواياه دائماً 180 درجة.[٢]
أمثلة على حساب محيط المثلث
المثال الأول:
يبين المثال التالي طريقة حساب محيط المثلث مختلف الأضلاع:[٣]
السؤال: احسب محيط المثلث ذي الأضلاع: 11 سم، 9 سم، 5 سم؟
الحل: محيط المثلث= 9 سم+11 سم+5 سم= 25 سم.
المثال الثاني:
يبين المثال التالي طريقة حساب محيط المثلث متساوي الأضلاع:[٣]
السؤال: احسب محيط المثلث متساوي الأضلاع الذي يبلغ طول كل ضلع من أضلاعه 4 سم؟
الحل: يمتلك المثلث ثلاثة أضلاع متساوية طول كل منها 4 سم، وبالتالي محيط المثلث=4×3=12سم.
المثال الثالث
يبين المثال التالي طريقة حساب محيط المثلث قائم الزاوية، مع استخدام نظرية فيثاغورس وظل الزاوية لإيجاد أطوال الأضلاع المفقودة أولاً:[١]
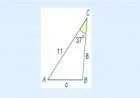
السؤال: مثلث قائم الزاوية، يبلغ طول أحد سيقانه ب= 5، ويبلغ قياس الزاوية المحصورة بين وتر المثلث وهذه الساق 28 درجة، فما هو محيط المثلث؟
الحل:
أولاً: لإيجاد الأضلاع المفقودة للمثلث نحتاج إلى القيام بالعمليات الحسابية التالية:
-
- افتراض طول الساق المفقود هي أ، فيكون ظا (28)= أ/5=0.5317 تقريباً، ومنها أ=2.6585.
- حساب طول الوتر باستخدام نظرية فيثاغورس، وهي نظرية هندسية معروفة، تنص على أن مجموع مربعات سيقان المثلث قائم الزاوية يساوي مربع الوتر، أي أن أ2+ب2=ج2[٤]: ومنها الوتر=الجذر التربيعي (أ2+ب2)=الجذر التربيعي 22.6585+25=5.6628 تقريباً.
- ثانياً: حساب محيط المثلث عن طرق جمع أطوال الأضلاع الثلاث:
- المحيط=5+5.6628+2.6585=13.3213 وحدات.
أنواع المثلثات
- أنواع المثلثات حسب عدد الزوايا والأضلاع المتساوية:[٢]
- المثلث متساوي الأضلاع: وهو يمتلك ثلاثة أضلاع متساوية، وثلاث زوايا متساوية وتساوي 60 درجة.
- المثلث متساوي الساقين: وهو يمتلك ضلعين متساويين، وزاويتين متساويتين.
- المثلث مختلف الأضلاع: وهو يمتلك أضلاعاً وزوايا مختلفة وغير متساوية.
- أنواع المثلثات حسب أنواع الزوايا داخله:[٢]
- المثلث حاد الزوايا: جميع زواياه أقل من 90 درجة.
- المثلث قائم الزاوية: وهو يمتلك زاوية قائمة تساوي 90 درجة.
- المثلث منفرج الزاوية: وهو يمتلك زاوية أكبر من 90 درجة.
- من الجدير بالذكر أن المثلث قد يمتلك اسمين معاً؛ مثل المثلث قائم الزاوية ومتساوي الأضلاع.[٢]
المراجع
- ^ أ ب "Perimeter of a Triangle"، www.tutorvista.com، Retrieved 24-10-2017. Edited.
- ^ أ ب ت ث "Triangles"، www.mathsisfun.com، Retrieved 24-10-2017. Edited.
- ^ أ ب "Perimeter"، www.mathgoodies.com، Retrieved 25-10-2017. Edited.
- ↑ The Editors of Encyclopædia Britannica، "Pythagorean theorem"، www.britannica.com، Retrieved 25-10-2017. Edited.