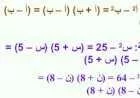محتويات
كيفيّة حل المُعادلة الجبريّة
إنّ حل المُعادلة الجبريّة هو الرّقم الذي يُمكن وضعه مكان المُتغيّر لإنتاج تعبيراً صحيحاً، وعلى الرّغم من عدم وجود طريقة مثاليّة لحل المُعادلات الجبريّة، إلّا أنّ وضع المُتغيّر وحده كهدفٍ لحل المعادلة من الطرق الجيّدة للنجاح في حل المعادلة، حيث تُصبح صيغة المعادلة كالتالي: س=رقم، وما يلي خطوات حل المعادلة التّالية؛ 4س-6=6:[١]
- ننقل الرّقم 6 من الطرف الأوّل إلى الطّرف الآخر، وسيؤدّي ذلك إلى تغيير إشارته، وتُصبح المعادلة كالتالي: 4س=6+6؛ أي 4س=12.
- نُقسم طرفيّ المعادلة على العدد 4، لنتخلّص من معامل س كالآتي: 4س/4=12/4، وتُصبح المعادلة س=3، وبالتالي فإنّ ناتج المعادلة هو العدد 3.
حلول المُعادلات الجبريّة
يُطلق على قيم المُتغيّرات التي تُنتج تعبيراً رياضيّاً صحيحاً اسم حلول المعادلة، وما يلي أنواع حلول المعادلات الجبريّة:[٢]
المُعادلات التي لها حلّاً واحداً
على سبيل المثال تمتلك المُعادلة التّالية 3أ+5=8 حلّاً واحداً، حيث إنّ قيمة (أ)=1 فقط.
المُعادلات التي لها عدد لا نهائيّ من الحلول
يُمكن أن تمتلك المعادلة التّالية: س=س عدداً لا نهائيّاً من الحلول، وذلك لأنّ قيمة س قد تكون أي رقماً من الأرقام.
المُعادلات التي ليس لها حلول
هُناك مُعادلات لا يوجد لها حلول بسبب عدم تساوي طرفيّها أبداً، فعلى سبيل المثال ليس هناك حلولاً للمعادلة التّالية: س+5=س+6، حيث إنّ محاولة إعطاء المجهول (س) قيمة تجعل طرفيّ المُعادلة غير متساويين دائماً، فعلى سبيل المثال إذا كانت قيمة (س) تساوي 1، فإنّ المُعادلة ستُصبح 1+5=1+6؛ أي 6=7 وذلك ليس صحيحاً.
المُعادلات الجبريّة
يُطلق على العمليّة الحِسابيّة التي يُعبّر عنها عن طريق صياغة تعبيران جبريّان بينهما مساواة باستخدام العمليّات الجبريّة المختلفة كالجمع، والطّرح، والقسمة، والضّرب، واستخراج الجذر، والرّفع إلى قوة المُطبّقة على مجموعةٍ من المتغيّرات اسم المعادلة الجبريّة (بالإنجليزيّة: Algebraic equation)، ويوجد حالات خاصّة من المعادلات الجبريّة ككثيرات الحدود (بالإنجليزيّة: polynomial equations)، حيث يتميّز هذا النّوع بامتلاكه العديد من الحلول.[٣]