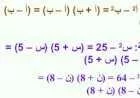طرق حل المعادلة الأسية

طرق حل المعادلة الأسية

عند التعامل مع معادلة أُسِّية مثل هذه المعادلة (4x=16) حيث الحرف x يمثل الأس (القوة) المقرونة بالعدد 4، فإنّ السؤال الذي يتبادر لذهن الشخص ما القيمة التي سيكون عليها الأس والتي ستجعل من الرقم 4 يساوي 16، وبالتالي فإنّ الإجابة ستكون أنّه حين يتكرر الرقم 4 مرتين (أي يُضرب بنفسه مرتين) فإن النتيجة ستؤول إلى 16 ومنه ستكون قيمة الأس (2)، ومن ناحية أخرى فإننا حين نقوم بحل المعادلات الجبرية، فإن الفكرة التي تسود في عقولنا هي إمكانية التعديل على قيم كلاً من الجهتين (على يمين ويسار إشارة اليساوي) بنفس المعدل من التغيير لكي تبقى الكفتين متساويتين وهو ما ينطبق أيضاً على المعادلات اللوغاريتيمة، فلو أعدنا النظر للمعادلة السابقة فيمكن حلها باستخدام اللوغاريتم العشري أو باللوغاريتم الطبيعي كما في التفصيل التالي الذي سنستخدم فيه اللوغاريتم الطبيعي:^[١]

• 4x=16← حين نطبق اللوغاريتم على كلا الجهتين يصبح لدينا ←log 4x=log 16 (عندما نضع اللوغاريتم بحالته العادية غير مقرون بأي قيمة فهذا يعني أنّ قيمة القاعدة تساوي 10)
• باستخدام خصائص اللوغاريتم الأسية تصبح المعادلة كالآتي: ←xlog 4=log 16 ومنه قيمة (x=log 16÷log 41.204÷0.602=2) (وهي قيمة الأس x).
• لو أردنا تعقيد المعادلة بعض الشيء كأن نجعل صيغتها كالآتي: (4x 17) حيث (x) هو الأس، فإنّ خطوات الحل ستكون كما في المثال السابق، ولكن الخطوة الأخيرة ستكون (x=log 17÷log 4→x=1.230÷0.602 2.-43).
• لو أردنا حل مسألة أخرى أكثر تعقيداً باستخدام اللوغاريتم الطبيعي، فستكون الطريقة كالآتي: e2x=54→ln e2x=ln 54→2x =ln 54→x=ln 54÷2→x=1.99449
• لو أخذنا المثال التالي الذي فيه القاعدة (الرقم 3) متساوية والدرجة الأسية متساوية أيضاً كما في المثال (32x+5=33x–2) حيث الأسس هنا عالتوالي (2x+5) و(3x–2) فإنّ الحل سيكون بالتعامل مع الأسس نفسها و إهمال القواعد (الرقم 3) لأنّها متساوية كما في الآتي: (2x+5=3x–2→5=x–2→(7=x، أما في حالة تساوي الأسس بالقيمة واختلاف القواعد كما في (x+4) (8)=(7) (8) حيث الأس يساوي 8 فسوف نهمل الأسس لتساويها ونتعامل مع القواعد فقط كما في الآتي: x+4=7→x=3.

مهارات الرياضيات

يتعين على أي طالب أو أي مهتم بعلم الرياضيات أن تتوفر عنده مهارات فنية لكي يتعامل بشكل مثالي مع الرياضيات، ومن هذه المهارات نذكر ما يلي:^[٢]

• مهارة التفكير الناقد.
• مهارة حل المسائل الرياضية.
• مهارة التفكير التحليلي.
• مهارة المنطق الكمِّي.
• مهارة التلاعب بأفكار دقيقة ومعقدة.
• مهارة بناء الحجج المنطقية وفضح الحجج غير المنطقية.
• مهارة التواصل.
• مهارة إدارة الوقت.
• مهارة العمل ضمن الفريق الواحد.

تعريف علم الرياضيات

تُعَرَّف الرياضيات على أنّها العلم الذي يشتمل على أسس رئيسية (القياس والعد والوصف الدقيق للأشكال الهندسية) والذي يتعامل مع الحساب الكمي والتفكير المنطقي، وقد أثرى تطور الرياضيات في زيادة مستوى المثالية والتجريد من موضوعها، حتى أنّها (الرياضيات) ومنذ القرن السابع عشر كانت مكمِّلة لا غنى عنها للعلوم والتكنولوجيا الفيزيائية، وفي الآونة الأخيرة اضطلعت بدور مماثل في الجوانب الكمية من علوم الحياة.^[٣]

المراجع

1. ↑ "Solving Exponential and Logarithmic Equations", montereyinstitute, Retrieved 21-8-2018. Edited.
2. ↑ "Where Can Math take me? ", uky, Retrieved 21-8-2018. Edited.
3. ↑ Menso Folkerts John L. Berggren Craig G. Fraser Wilbur R. Knorr Jeremy John Gray, "Mathematics"، britannica, Retrieved 21-8-2018. Edited.